Bei Streifzügen durch die MOOC-Welt, Statistiktutorials auf YouTube oder kleinen Programmierselbsthilfeforen stoße ich in letzter Zeit wiederholt auf eine Wortwendung, die mich aber schon immer verwirrt hat: die steile Lernkurve oder vielmehr — da die meisten Onlineangebote auf Englisch vorhanden sind — die der steep learning curve.
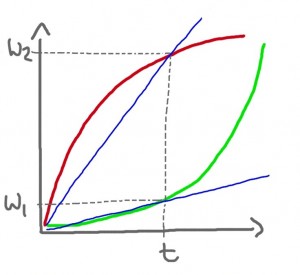
Denn ganz offensichtlich warnen alle Dozierenden davor, Kurse und Programme zu unterschätzen: „It will be hard work, as R initially has a steep learning curve“ (‚Es ist harte Arbeit, weil R am Anfang eine steile Lernkurve hat‘). Zu den emotionalen Hürden beim Erlernen einer Programmiersprache mach(t)e ich mir ja keine Illusionen. Was mich aber immer verwirrt hat, war der unklare Bezug des Adjektivs steil. Denn die vielen, vielen Verwendung von steep learning curve suggerieren sofort, dass der Zeitaufwand (t) hoch, der Wissensgewinn (w) aber anfangs frustrierend gering ist. Würde man das aufmalen wollen, wäre die Warnung in diesem Diagramm durch die grüne Linie repräsentiert:
Aber was soll an der grünen Linie besonders steil sein, so zum Anfang? Zum Zeitpunkt (t) habe ich mir nur Wissen (w1) angeeignet. Steil ist dabei doch höchstens die rote Linie, die aber genau das Gegenteil zeigt, nämlich, dass man sich in kürzerer Zeit (t) relativ viel Wissen (w2) aneignen kann. Wollen die mir mit dunkler Weltuntergangsstimme sagen, dass man mit wenig Zeit viel erreicht? Dass man also vor einer Lernkurve warnt, weil sie schnellen Lernerfolg verspricht?
Da stimmt doch was nicht.
Die erste logische Anlaufstelle Wikipedia weiß Bescheid: dort spricht man von einer „akademischen“ Verwendung der Redewendung (Stoffmenge in Abhängigkeit von Zeit, rote Linie) und einem umgangssprachlichen Verständnis, das der „akademisch als korrekt zu betrachtenden Definition“ „diametral“ gegenüber steht. Letzteres entspricht zwar nicht ganz meiner grünkurvig dargestellten Verwirrung, diese ist aber immerhin diametral. ((Auf Wikipedia korreliert man das Laienverständnis mit der sogenannten Blender-Kurve, welche mit anderen Variablen hantiert, die aber, drehte man die Achsen sinnvoll um, in groben Kurven der grünen Linie in Abbildung 1 entspräche.)) Ist das wirklich nur ein weiteres Beispiel dafür, dass Fach- und allgemeiner Sprachgebrauch nicht übereinstimmen, wenn auch ein besonders extremes?
Nein. Das Durchforsten von Korpora und der Versuch, learning curve ein quantitatives Muster abzuringen, bringen’s ans Licht: hier werden Äpfel und Birnen als Orangen bezeichnet.
Zunächst: Die akademische Interpretation ist zweifellos die mathematische Funktion w(t). Dass man von einer steilen Lernkurve spricht, liegt daran, dass wir das Mehr an Quantität (hier: Lernerfolg) über die Zeit mit einer nach oben gerichteten Linie mit großer ‚Steigung‘ illustrieren. Man kennt diese Darstellung beispielsweise von Börsenkursen: Kursgewinne zeigen nach oben, Verluste nach unten. Solche Diagrammformen sind dabei letztendlich reine Konvention, weil man ja lediglich die mathematische Abhängigkeit einer Variablen von einer anderen abbildet — man könnte das Diagramm um 180° oder auch nur um 90° drehen, ohne Informationsgehalt einzubüßen. Aber dass diese anschauliche Darstellung die intuitivere Konvention ist, liegt daran, dass unsere Wahrnehmung allgemein von der konzeptuellen Metapher MEHR IST OBEN (MORE IS UP) geprägt ist, die auf Erfahrung mit unserer Umwelt basiert: je höher der Stapel Klausuren auf meinem Schreibtisch, desto mehr habe ich zu tun. Deshalb nehmen wir diese Kurven als steil wahr, obwohl steil ja nur ihre Darstellung ist.
Der umgangssprachlichen Verwendung für steile Lernkurve liegt eine ganz ähnliche Motivation zugrunde, die gegenüber der hilfsweisen Darstellung der mathematischen Funktion aber grundlegend metaphorisch ist. Was meinen wir damit? Schauen wir zur Erklärung mal ein paar Beispiele aus dem Corpus of Contemporary American English (COCA) an:
Overall, you’ll face a fairly steep learning curve to master OpenOffice’s eccentricities, but you can’t beat the price.
[Insgesamt haben Sie eine recht steile Lernkurve vor sich, um die Verschrobenheiten von OpenOffice zu meistern, aber der Preis ist unschlagbar.]
„Anybody who rides a mountain bike wants to do what we do, but there’s a really steep learning curve so they usually end up just watching,“ he says.
[„Jede/r, der/die ein Mountainbike fährt, möchte machen, was wir machen, aber das hat eine wirklich steile Lernkurve, weshalb sie meistens nur zusehen.“]
„second Life provides an additional way for students to explore class material, but it doesn’t appeal to everyone.“ A steep learning curve can also discourage students who are not highly motivated to use SL, he says.
[„second Life stellt zusätzliche Möglichkeiten für Studierende bereit, um das Kursmaterial zu erkunden, aber das ist nicht für jede/n attraktiv.“ Eine steile Lernkurve kann Studierende zusätzlich entmutigen, die wenig motiviert sind, SL zu nutzen, sagt er.]
Nahezu alle Belege für learning curve hauen in die gleiche Kerbe: Lernen ist mühsam, aufwändig, anstrengend, mitunter entmutigend. Es überrascht nicht, dass das Nomen learning curve nur ein einziges signifikantes Adjektivkollokat hat: steep. ((Für diese Erkenntnis haben Daten aus der Kollokationsdatenbank des British National Corpus (via BNCweb) hergehalten. Spannweiten von 1;0 bis 5;5. Der Server für COCA ist gerade unten, aber am Wochenende hab ich mir von dort noch schwache Assoziationen zu efficient, upward, shallow und sharp notiert.)) Umgekehrt modifiziert steep — das wird niemanden vom Hocker hauen — überwiegend Nomina der Erhöhung oder des Aufstiegs wie hill, climb, ridgery, rise oder ascent. ((In der Kollokationsliste stehen auch Begriffe der absteigenden Richtung wie cliff, slope, decline oder descent.)) Wir assoziieren Lernen also mit einem Weg (nach oben) zur Erkenntnis. Eine andere Perspektive auf die Beschwerlichkeitskonnotation für steep learning curve ist, dass es häufig in Strukturen auftaucht, die mit dem Verb to face ‚gegenüberstehen‘ eingeleitet werden. In solchen face-Konstruktionen stehen in der Objektposition wiederum signifikant häufig challenges, risks, problems, obstacles, hardships, dilemmas und problems, also eher weniger spaßige Dinge.
Die negative Perspektive aufs Lernen ist auch in der Wikipedia-Definition erwähnt. Dort hat man versucht, die mathematische Definition als positive, die Laienverwendung als negative Einstellung zu deuten. Das ist nicht ganz falsch (abgesehen davon, dass eine mathematisch-quantitative relativ wenig mit ‚positiv‘ oder ‚Einstellung‘ zu tun hat), aber eben eine ungünstige Vermischung von Ebenen. Aber jetzt — um auf die Äpfel und Orangen zurück zu kommen — können wir die Laienverwendung auf konzeptuellen Metaphern zurückführen, also auf die grundlegende kognitiven Strategie, abstrakte Dinge durch greifbare, konkrete Dingen zu konzeptualisieren. Eine bekannte und hier naheliegende, übergeordnete Metapher wäre DAS LEBEN IST EINE REISE (LIFE IS A JOURNEY). Und auf dieser Reihe geht es auf dem WEG zur Erkenntnis eben auch mal mühsam nach oben. Wen diese Idee interessiert, findet in Lakoff & Johnson (1980a, 1980b) eine äußert dankbare Lektüre. Wer mehr so auf bunte Bildchen steht:
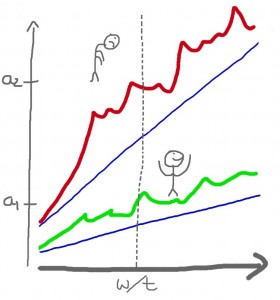
Bei der steilen Lernkurve steht nicht der Lernerfolg an sich im Vordergrund (oder dessen Quantifizierung), sondern die Anstrengung a: wenn ich auf dem grünen Pfad mit der flacheren Lernkurve unterwegs bin, hab ich zum Zeitpunkt t (oder wahlweise zum Wissenstand w) mit a1 weniger Anstrengung hinter mir, als wenn ich die rote Route (steile Lernkurve) nehmen muss. Konkrete, physische Empfindungen während einer anstrengenden Bergbesteigung oder eines flauschigen Hügelspaziergangs dienen uns dabei als Quelle zur Verbalisierung abstrakter Emotionen während einer Lernerfahrung. Die Y‑Achse ist zur Verdeutlichung eingezogen: bei der WEG/REISE-Metapher spielt die Quantifizierung — und streitbarerweise sogar der Betrag des Wissenstands — nur eine untergeordnete Rolle. Was bei Lernkurven interessiert ist der Grinsegrad auf dem Weg zur Erkenntnis zum Zeitpunkt t.
Denn wenn ich heute sage, dass R für eine funktionale Technikanalphabetin ne steile Lernkurve hat, sage ich doch überhaupt nichts darüber aus, ob die R‑onautinnen-Ausbildung quantitativ bei mir gefruchtet hat oder nicht.
P.S.: Fürs Deutsche ist die Metaphernstrategie der steilen Lernkurve ähnlich, wenn auch quantitativ offenbar nicht so stark messbar. Als einzige sinnvolle Kollokate spuckt COSMASII aus dem Deutschen Referenzkorpus (DeReKo) steil, flach und — öbachtle! — PHP aus. Auch im DWDS sind signifikante Verbindungen für Lernkurve mit lediglich schwachen Assoziationen zu steil eher mager (aber DWDS & DeReKo mit BNC & COCA vergleichen zu wollen, ist für diese Untersuchung ohnehin problematisch). Das Wortschatzportal der Universität Leipzig liefert als auffällige Verbindung rechts von Lernkurve außerdem vor sich, was auf die WEG-Metapher hinweist (sie haben einen weiten Weg vor sich). Der Eindruck ist aber ein wenig, dass die Bergsteigemetapher im Deutschen schwächer ausgeprägt ist und bei Lernkurve häufiger vom mathematischen Konzept die Rede ist.
–
Lakoff, George & Mark Johnson. 1980a [2003]. Metaphors we live by. University of Chicago Press. [Auf Deutsch: Leben in Metaphern: Konstruktion und Gebrauch von Sprachbildern. Carl Auer Verlag.]
Lakoff, George & Mark Johnson. 1980b. Conceptual metaphor in everyday language. Journal of Philosophy 77(8). 453–486. [Link]

Ich habe mir unter einer steep learning curve immer vorgestellt, daß man in einem bestimmten Kurs oder auch beim Erlernen einer bestimmten Tätigkeit anfangs sehr viele schwierige Dinge zugleich oder schnell hintereinander vorgesetzt bekommt bzw. meistern muß, also in der Tat w(t) sehr schnell ansteigt.
Ich hatte jetzt bisher immer angenommen, dass die damit nur sagen wollen, man müsse am Anfang halt sehr viel lernen, bevor man durchsteigt.
Wieder was gelernt.
Interessant. Ich habe die Formulierung “steile Lernkurve” immer als etwas positives wahrgenommen und auch in dieser Absicht verwendet. Eben um Dinge die auf den ersten Blick total kompliziert erscheinen, es gar nicht sind, sobald man anfängt sich damit zu beschäftigen. Und dann eben schnell Erfolge erzielt, also die rote Kurve (mir ging u.a. beim Lernen von LaTeX und Emacs so). Ich frage mich jetzt wieviele Menschen ich nun von z.B. LaTeX und Emacs abgeschreckt habe weil ich ihnen freudig eine steile Lernkurve versprochen habe 🙂
Du könntest auch einfach Aufwand (bzw. Zeit) über Wissen plotten, statt andersherum. Wenn die Frage ist, wie viel Arbeit ich investieren muss, um eine bestimmte Menge Wissen zu erreichen, lässt sich durchaus argumentieren, dass dann die Funktion a(w) ist. Dann hast du auch gleich deine steile Kurve..
Hm, aber liegt das nicht auch an der Art, wie Du die Grafen zeichnest?
Vergleichen wir mal die beiden hier:
*******************
***
**
**
**
*
*
*****************
***
***
***
Ich vermute, dass dieser Unterschied eher gemeint ist, als der von Dir skizzierte. Wenn ich zum Beispiel Photoshop im Unterschied zum mit Windows mitgeliefterten Paint erlerne, bin ich mit einer steilen Lernkurve konfrontiert: Am Anfang beherrsche ich fast nichts von dem, was ich wissen muss. (Das Plateau der Kurve liegt weit über mir.) Bei Paint ist das anders, ich brauche nur wenige, nicht allzu komplexe Lernschritte, um das vergleichsweise niedrige produktive Arbeitsniveau zu erreichen.
Mist, da hat mir WordPress die Leerzeichen vor den feinen Sternchen abgeschossen. Aber vielleicht lässt sich ja trotzdem erahnen, was meine ASCII Kunst hier darstellen sollte…
Huch! Und ich dachte mit der steilen Lernkurve sei gemeint, dass am Anfang noch alles recht einfach ist, man also sehr schnell zu Ergebnissen kommt (“Hello World” in Scriptsprachen, LaTeX mit Standardformatierungen etc.), das Erlernen der Feinheiten später dann aber recht lange dauert. Aber geschwurbelte Einleitungen irgendwelcher Lehrbücher überblättere ich auch gerne mal 😉
Meinst du in Abbildung 2 mit a wirklich die Anstrengung, oder eher sowas wie integrierte Anstrengung. So wir du es gezeichnet hast, ist es bei roter wie grüner Kurve zu Anfang wenig Anstregend und wird dann immer schlimmer. Ich würde eher annehmen, dass die Steigung und nicht die Höhe der Kurve die Anstrengung symbolisiert.
Ich hatte nie über die Diametrialität zwischen Bedeutung und Aussage der Redewendung Gedanken gemacht. Danke für diese Analyse.
Und die Zeichnungen haben meinen Tag verschönt! 😀
Die Analyse ist zwar sehr hübsch, aber die Verwunderung über die Schwierigkeit der steilen Lernkurve wird sofort aufgehoben, wenn man sie als “geforderte” Lernkurve versteht. Dann könnte man es allerdings auch besser als “Lehrkurve” bezeichnen.
So, jetzt widme ich mich nach dem Konferenzstress Euren Kommentaren:
@sPa/Muriel: ja, das ist ja auch nicht ganz verkehrt — vermischt nur beide Verständnisse des Begriffs.
@Turtle: die mathematische Interpretation sagt ja genau das aus — sehr schnell sehr viel lernen. Aber die negative, nicht-mathematische Konnotation könnte in der Tat eher dazu führen, dass man von LaTeX abgeschreckt wird. Deshalb war ich immer so verwirrt — weil da zwei Konzepte in verschiedene Richtungen zerren, irgendwie.
@h: ja, war nur nicht die Intention — die steile Lernkurve als konzeptuelle Interpretation des allgemeinen Sprachgebrauchs darzustellen. Wäre deine vorgeschlagene Lösung nicht die grüne Kurve von oben, nur mir vertauschten Achsen?
@Joachim: Ja, das ist in der Tat keine mathematische Darstellung. Das sollte mit der dünneren Linie symbolisiert sein.
@Wentus: auch hier: ja, darum geht’s aber nicht, wie der allgemeine Sprachgebrauch zeigt, wo die gefühlte Anstrengung im Vordergrund steht.
Laut Wikipedia-Eintrag gibt es neben der a.) korrekten Verwendung von “steiler Lernkurve” — also schneller Wissenserwerb am Anfang, der abflacht — auch eine b.) diametrale, widersprüchliche: mühsamer Wissenserwerb am Anfang, danach wird es leichter.
Ich denke, für die irreführende Verwendung b.) ist eine verschlimmbessernde Übersetzung eines Fachterminus verantwortlich. Es ist nämlich gar nicht die Lernkurve, die steil ist (die ist ja in Wahrheit flach), sondern die Progression. Progression ist ein Begriff aus der Didaktik, der die zu bewältigende Stoffmenge pro Zeiteinheit beschreibt. Eine steile Progression bedeutet somit ein schnelles Fortschreiten im Stoff. That’s it.
Die Erklärung der falschen Verwendungsweise mithilfe der konzeptuellen Metapher vom “steilen Weg” finde ich überzeugend, wenn ich auch eher anstelle des Lebensweges an eine Zielankunft bei der Tour de France denken würde. 😉
Offensichtlich kennen die vielen Falschverwender das Konzept der Lernkurve nicht, finden das Wort aber so schick, dass sie nicht darauf verzichten können. :-/
Grüße,
Jürgen
@Jürgen: genau das habe ich nicht gesagt, also dass das eine eine Falschverwendung ist. Es gibt zwei Verwendungen, denen zwei grundlegend unterschiedliche Metaphern zugrunde liegen.
Ergänzung: Bei einer steilen Progression sollte auch die Lernkurve steil sein können. Wenn das nicht so ist, müssen Lehrer oder Autoren von Lernwerken ihren Stoff eben schülergerechter auf die Unterrichtseinheiten oder Buchkapitel verteilen.
Also: Steile Progression und steile Lernkurve schließen sich keineswegs aus. Wenn aber die Lernkurve zu flach ist, war die Progression zu steil.
@Susanne
Das “falsch” ist tatsächlich meine Wertung, aber ich finde, dass du die, neutral gesprochen, zweite Verwendungsweise gut erklärt hast. “Falsch” finde ich die “steile Lernkurve” im Sinne von “sehr schwierig” insofern, als hier der Begriff der Lernkurve auf den Kopf gestellt wird.
Ich hab zwar wenig Sympathien für Sprachnormierer (Genitivfetischisten und ähnliche), bin aber ein großer Freund des Verständlichkeitsprinzips. Deshalb zögere ich nicht, Ausdrücke als “falsch” zu bezeichnen, in denen ein Wort (Lernkurve) das Gegenteil von dem üblicherweise damit Bezeichneten bedeutet.
Auch hier liegt ein Missverständnis vor, nämlich, dass es eine ‚eigentliche‘ und damit eine angeblich ‚übliche‘ Verwendung gäbe. Wenn ein genügend großer Teil der Sprachgemeinschaft — und das tut dieser Teil (siehe Daten, hier aus dem amerikanischen Englisch) — einen Ausdruck mit einer starken Tendenz zu A verwendet, dann kann A nicht „falsch“ sein. Das ist etwas grundlegend anderes, als Einzelfälle, bei denen genuin falsche, also der sprachgemeinschaftlichen Konvention widersprechende Verwendung vorliegt. Hier ist der unterschied eben zwischen einer Mathematischen und einer Allgemeinsprachlichen (das kommt häufig vor).
(Möglicherweise haben wir hier den Störfaktor „Muttersprache“, weil es im Deutschen mit der steilen Lernkurve anders aussieht, als im Englischen mit steep learning curve; fürs Deutsche zeigte sich die Tendenz nämlich nicht so deutlich.)
“Wenn ein genügend großer Teil der Sprachgemeinschaft (…) einen Ausdruck mit einer starken Tendenz zu A verwendet, dann kann A nicht ‘falsch’ sein.”
Du hast im Grunde recht, dieses Prinzip habe ich auch immer mit aller Verve gegen alle sog. “Sprachschützer” vertreten (Zwiebelfisch etc.). Nun ist aber in meinen Augen die zweite Verwendung von “steiler Lernkurve” eine solche, die, statt Verständigung zu ermöglichen, systematisch Missverständnisse erzeugt. Deshalb würde ich von der zweiten, nicht ursprünglichen Verwendung dieses Ausdrucks abraten.
Die Bedeutung von “Lernkurve” im fraglichen Ausdruck widerspricht zumindest der fachsprachlichen Verwendung — die ich allerdings bisher für die einzig mögliche und damit auch umgangssprachliche Verwendung hielt. Vielleicht hast du Recht damit, dass hier zwischen einem fachwissenschaftlichen (“mathematischen”) und einem alltagssprachlichen Gebrauch unterschieden werden muss. Auch die umgangssprachliche Lernkurve ist eine Lernkurve, halt nur eine andere, mit einem anderen Parameter auf der x‑Achse (“Anstrengung” statt “Stoffmenge” bzw. “Lernerfolg”).
Leider gibt es m.W. für die “steile Progression” (“viel Lernstoff am Anfang”) keinen Ausdruck der Umngangssprache, in dem “Lernkurve” nicht vorkommt. Das ist für alle ein großes Problem, die “steile Progression” oder “Lernkurve” als Fachbegriffe kennen und benutzen!
Grüße,
Jürge
Ein Aspekt, der meine (und deine) bisherige Argumentation völlig aufhebt: Beide Verwendungsweisen von “steiler Lernkurve” schließen sich nicht aus! Wenn ich z.B. eine neue Sprache lerne, dann bewältige ich in kurzer Zeit eine große Stoffmenge (Vokabeln und Grammatikregeln). Gleichzeitig kostet mich das aber auch viel Anstrengung.
Schnelligkeit ist oft erforderlich, um einen steilen Anstieg zu schaffen. Wer langsam mit dem Rad einen Berg hinauffahren möchte, weiß das. 😉 Liegt hier nicht die gemeinsame Wurzel der umgangssprachlichen Sichtweise?
“Was mich aber immer verwirrt hat, war der unklare Bezug des Adjektivs steil. Denn die vielen, vielen Verwendung von steep learning curve suggerieren sofort, dass der Zeitaufwand (t) hoch, der Wissensgewinn (w) aber anfangs frustrierend gering ist.”
Diese Suggestion liegt m.E. überhaupt nicht nahe, auch nicht bei den von aufgeführten Beispielen. Immer ergibt sich hier die hohe Anstrengung zum Beginn der Lernphase aus der Notwendigkeit, viel Wissen in kurzer Zeit zu erwerben. Anstrengung und Wissenserwerb korrelieren also.
Spricht man tatsächlich auch bei einem Lernstoff, der nur geduldig in kleinen Häppchen erworben werden kann, von “steiler Progression”? Wo sich also Anstrengung _nicht_ in schnelleren Lernerfolg überträgt?
Grüße,
Jürgen