Da wende ich dem Wissenschaftsfeuilleton nur kurz den Rücken zu, um mich ein paar Tage lang auf einer der wichtigsten Konferenzen der deutschen Sprachwissenschaft herumzutreiben, und verpasse dabei glatt die sprachwissenschaftliche Sensation des Jahrhunderts. Holger Dambeck weiß auf Spiegel Online nämlich Folgendes zu berichten:
So sehr sich amerikanische und europäische Kinder in Mathe-Tests anstrengen – ihre Altersgenossen aus China sind besser. Dank eines einfacheren Zahlensystems können sie schon früh besser zählen und rechnen. Sprachforscher glauben, dass die Methodik auch deutschen Kindern helfen würde. [SPIEGEL.de/Dambeck 2010]
Bevor ich erklären kann, was daran eine Sensation wäre, muss ich erklären (wie es auch der Artikel tut), was mit einem „einfacheren“ Zahlensystem gemeint sein soll: nämlich ein System sprachlicher Ausdrücke, das sich möglichst streng an der Dezimalschreibweise orientiert. In dieser Schreibweise gibt es, wie wir alle wissen, eigene Symbole für die Zahlen von Null bis Neun, ab der Zehn werden alle Zahlen als Kombination dieser Symbole geschrieben, in der Einer, Zehner, Hunderter, usw. in absteigender Reihenfolge genannt werden. Die Zahl „Einhundertfünfzehn“ etwa wird 115 geschrieben, was ja soviel heißt wie „Ein Mal Hundert, und ein Mal Zehn, und fünf Mal eins“.
Im Deutschen und Englischen (und in vielen anderen Sprachen) folgt die Sprache dieser Logik aber nicht: das Wort einhundertfünfzehn nennt erst die Hunderter (einhundert-), dann die Einer (-fünf-) und dann die Zehner (-zehn). Im Chinesischen ist das anders, hier folgt die Sprache streng der Dezimalschreibweise, das Wort für 115 ist „Eins-Hundert-Eins-Zehn-Fünf“ (yi1 bai3 yi1 shi2 wu3).
Ein weiterer Unterschied zwischen dem Chinesischen auf der einen und dem Englischen und Deutschen auf der anderen Seite findet sich im Zahlenraum zwischen Zehn und Zwanzig. Hier haben das Englische und Deutsche für einige Zahlen ganz eigene Wörter, bei anderen Wörtern ist zwar eine Verwandtschaft zu den Zahlwörtern für die einzelnen Teile sichtbar, aber die Formen sind trotzdem nicht identisch. Ganz eigene Wörter gibt es für die 11 und die 12. Die 11 beispielsweise müsste die nach der Logik des Zahlensystems im Deutschen eigentlich „einszehn“ (vgl. dreizehn oder „einundzehn“ (vgl. einundzwanzig) und im Englischen „ten-one“ (vgl. twenty-one) heißen, tatsächlich aber heißt sie völlig intransparent elf bzw. eleven.
Ein Beispiel für eine verwandte aber trotzdem eigene Form im Deutschen wäre das Wort für 17, das eigentlich siebenzehn oder siebenundzehn lauten müsste, bei dem die zweite Silbe des Wortes sieben aber fehlt (siebzehn). Im Englischen sind alle Zehner nur teilweise nachvollziehbar, weil statt des erwarteten ten das entfernt ähnlich klingende teen verwendet wird. Außerdem gibt es auch hier bei den Einern Unregelmäßigkeiten: 13 heißt thirteen statt threeteen und 15 heißt fifteen statt fiveteen. Das Chinesische verfährt in diesem Zahlenraum völlig regelmäßig: 13 heißt z.B. „zehn-drei“ (shi2 san1), fünfzehn heißt „zehn-fünf“ (shi2 wu3), und siebzehn heißt „zehn-sieben“ (shi2 qi1).
Ein letzter Unterschied besteht darin, dass das Englische und Deutsche für die Zehner Wörter haben, die zwar mit den entsprechenden Einern sprachlich verwandt sind, die aber trotzdem oft eigene Formen darstellen: Dreißig ist transparent mit dem Wort Drei verwandt, aber Zwanzig nur entfernt mit dem Wort Zwei; auf ähnliche Weise ist z.B. das Englische sixty klar erkennbar mit six verwandt, aber thirty nur entfernt mit three. Außerdem haben -zig und -ty lautlich nur wenig mit zehn gemein. Im Chinesischen gibt es dagegen keine eigenen Wörter für die Zehner: Zwanzig ist „Zwei-Zehn“ (er4 shi2), Dreißig „Drei-Zehn“ (san1 shi2), und so weiter.
Schließlich ist noch interessant, dass das Englische sich wenigstens im Zahlenraum ab Zwanzig an der Dezimalschreibweise orientiert (21 ist z.B. twenty-one, das Deutsche aber bei der umgekehrten Reihenfolge bleibt und den Einer zuerst nennt (einundzwanzig).
Und diese streng an der Dezimalschreibweise orientierten chinesischen Zahlwörter, so der Artikel, seien der Grund dafür, dass chinesische Kinder weiter zählen und besser rechnen können, als ihre amerikanischen oder deutschen Altersgenossen. Der Artikel nennt sogar die Quelle für diese Behauptung: eine Studie des amerikanischen Psychologen Kevin Miller aus dem Jahr 1995 (er verlinkt lobenswerterweise sogar auf die Studie, allerdings ist ein Zugang zum Archivdienst JSTOR notwendig).
Nun zur Sensation: Wenn man zeigen könnte, dass die Wörter für Zahlen in einer bestimmten Sprache einen Einfluss auf die Rechenfähigkeit ihrer Sprecher haben, wäre das ein klarer Beleg für sprachliche Relativität, also für die Hypothese, dass die Struktur unserer Sprache unser Denken beeinflusst. Es wäre sogar ein Beleg für eine besonders starke Version dieser These, die seit Willhelm von Humboldt kein ernstzunehmender Sprachwissenschaftler vertreten hat — dass nämlich unterschiedliche Sprachen nicht nur ein unterschiedliches, sondern ein unterschiedlich gutes Denken ermöglichen.
Humboldt war aus mir nicht nachvollziehbaren Gründen der Meinung, dass flektierende Sprachen (also Sprachen, bei denen z.B. Verben gebeugt werden, um Zeitformen, Person usw. anzuzeigen), vollkommener seien als nicht-flektierende Sprachen. Von den ihm bekannten Sprachen schien ihm das Sanskrit dem Idealtyp einer flektierenden Sprache sehr nahe zu kommen, das Chinesische dagegen eher weit entfernt zu sein [Humboldt 1836, S. 301ff.]. Entscheidend ist, dass Humboldt aus diesen Unterschieden im Sprachbau auf die Leichtigkeit schloss, mit der die Sprecher der betreffenden Sprachen intellektuelle Leistungen vollbringen könnten:
Allein der wahre Vorzug der Sprachen muss doch in ihrer allseitig und harmonisch einwirkenden Kraft gesucht werden. Sie sind Werkzeuge, deren die geistige Thätigkeit bedarf, Bahnen in welchen sie fortrollt. Sie sind daher nur dann wahrhaft wohlthätig, wenn sie dieselbe nach jeder Richtung hin erleichternd und begeisternd begleiten, sie in den Mittelpunkt versetzen, aus welchem sich jede ihrer einzelnen Gattungen harmonisch entfaltet. Wenn man daher auch gern zugesteht, dass die Form der Chinesischen Sprache mehr als vielleicht irgend eine andere, die Kraft des reinen Gedanken herausstellt, und die Seele, gerade weil sie alle kleinen störenden Verbindungslaute abschneidet, ausschliesslicher und gespannter auf denselben hinrichtet, wenn die Lesung auch nur weniger Chinesischer Texte diese Überzeugung bis zur Bewunderung steigert, so dürften doch auch die entschiedensten Vertheidiger dieser Sprache schwerlich behaupten, dass sie die geistige Thätigkeit zu dem wahren Mittelpunkt hinlenkt, aus dem Dichtung und Philosophie, wissenschaftliche Forschung und beredter Vortrag gleich willig emporblühen. [Humboldt 1836, S. 301ff.]
Benjamin Lee Whorf, der in der ersten Hälfte des letzten Jahrhunderts die Idee der sprachlichen Relativität populär machte, schloss dagegen die Möglichkeit von „Qualitätsunterschieden“ zwischen Sprachen aus. Auch er war der Meinung, dass die Sprache, die wir sprechen, einen Einfluss auf unser Denken hat, er betrachtete aber alle sich daraus ergebenen Denkweisen als gleichwertig:
Western culture has made, through language, a provisional analysis of reality and, without correctives, holds resolutely to that analysis as final. The only correctives lie in all those other tongues which by aeons of independent evolution have arrived at different, but equally logical, provisional analyses. [Whorf 1956 (1941), S. 244]
(Die westliche Kultur hat durch Sprache eine vorläufige Analyse der Wirklichkeit vorgenommen und hält diese in Abwesenheit eines Korrektivs für endgültig. Das einzige Korrektiv liegt in all jenen anderen Sprachen, die durch Äonen unabhängiger Entwicklung zu anderen, ebenso logischen provisorischen Analysen gelangt sind.)
Nun gibt es durchaus Belege für eine sehr schwache Version der Whorfschen Relativitätshypothese: Unter sorgfältig kontrollierten Bedingungen lässt sich in einigen Fällen nachweisen, dass die Struktur einer Sprache einen kleinen Einfluss auf bestimmte Kategorisierungsvorgänge ihrer Sprecher hat.
Aber unterschiedliche Rechenfertigkeiten in einer nicht-kontrollierten Umgebung wie einer Schule wären ein Beleg, der deutlich über solche schwachen Effekte hinausginge und Humboldt Recht geben würde — nur, dass es im Falle der Mathematik dann gerade das Chinesische wäre, das „die geistige Thätigkeit zu dem wahren Mittelpunkt hinlenkt“.
Die Studie selbst ist dann aber ernüchternd: Kevin Miller und seine Kolleg/innen belegen dort keineswegs, dass die mathematische Leistungsfähigkeit von Sprechern einer Sprache irgendetwas mit der Versprachlichung des Zahlenraums zu tun hat.
Was sie sehr schön zeigen, ist, dass chinesische Kinder sich leichter tun als ihre amerikanischen Altersgenossen, wenn sie gebeten werden, so weit zu zählen, wie sie können: Die chinesischen Kinder haben gerade im Zahlenraum zwischen zehn und zwanzig weniger Probleme als die amerikanischen und sie können deshalb generell weiter zählen:
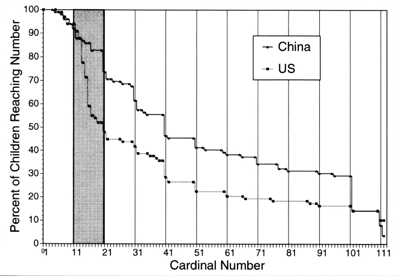
Anteil chinesischer und amerikanischer Kinder zwischen 3 und 5 Jahren, die bis zu einer bestimmten Zahl zählen können (Miller et al. 1995: 58).
Das Ergebnis ist interessant, aber mit unterschiedlichen mathematischen Fähigkeiten, und damit auch mit sprachlicher Relativität, hat es natürlich nichts zu tun. Es ist klar, dass das chinesische System leichter zu lernen ist und dass man, wenn man es einmal verstanden hat, problemlos bis 100 zählen kann, ohne verstanden zu haben, was Zahlen überhaupt sind. Meine vierjährige Tochter kann (wenn ich sie lasse) bis 1000 zählen, weil sie verstanden hat, wie man die Wörter kombinieren muss, um die sprachliche Bezeichnung für die jeweils nächsthöhere Zahl zu bilden. Sie kann aber nicht sagen, ob „dreihundertsiebenundsechzig“ mehr ist als „fünfhundertdreizehn“, weil sie im Zahlenraum ab 20 keine genaue Vorstellung mehr davon hat, wofür diese sprachlichen Bezeichnungen eigentlich stehen.
Die Autoren zeigen weiter, dass es chinesischen Kindern leichter fällt, im Zahlenraum zwischen zehn und zwanzig konkrete Objekte abzuzählen. Sie wurden aufgefordert, aus einem Topf eine bestimmte Zahl von Dominosteinen herauszunehmen und machten dabei weniger Fehler als die amerikanische Vergleichsgruppe. Das ist schon interessanter, da es hier nicht um ein reines Sprachspiel geht, sondern die Zahlen auf Mengen in der Welt bezogen werden. Mit Denk- oder Rechenfähigkeit hat das aber wieder nichts zu tun: Es erfordert nur, dass Kinder beim Hochzählen für jede Zahl einen Dominostein nehmen. Wenn sie beim Zählen keine Fehler machen, haben sie am Ende die korrekte Zahl an Steinen.
Die Autoren haben den Kindern anscheinend auch einfache Rechenaufgaben gestellt, gehen aber nicht weiter darauf ein, was für Aufgaben das waren. Sie stellen aber klar, dass es bei der Lösung dieser Aufgaben keine Unterschiede zwischen den Sprachen gab:
Despite large language effects on abstract counting, no language differences were found in children’s ability to solve simple mathematical problems or to count arrays of 10 or fewer objects. Both tasks are difficult for young children, but neither revealed language differences. [Miller et al. 1995: 58]
(Trotz eines großen sprachlichen Einflusses auf abstraktes Zählen wurden keine Unterschiede in der Fähigkeit der Kinder beobachtet, einfache mathematische Aufgaben zu lösen oder Gruppen von zehn oder weniger Objekten abzuzählen. Beide Aufgaben bereiten kleinen Kindern Schwierigkeiten, aber bei keinem gab es Unterschiede zwischen den Sprachen.)
Damit erübrigt es sich auch, den Verein Zwanzigeins e.V. zu erwähnen. Dessen Vorsitzender, der emeritierte Mathematikprofessor Lothar Gerritzen von der Ruhr-Universität Bochum hat dem Spiegel-Online-Autor die ganze Geschichte eingeredet: Er rührt nämlich seit Jahren ernsthaft die Werbetrommel für eine Reform unserer Zahlenwörter, bei der die Zahlwörter ab Zwanzig nach Vorbild des Chinesischen oder Englischen gebildet werden sollen — statt einundzwanzig sollen wir zwanzigeins sagen.
Statt über diesen VDS für Zahlennörgler zu reden, könnte man darauf hinweisen, dass die Franzosen ein wahrhaft pathologisches Zahlwörtersystem haben. Die Zahlen von 1 bis 16 haben eigene Namen, die Zahlen von 17 bis 19 werden transparent zusammengesetzt (dix-sept „zehn-sieben“, dix-huit „zehn-acht“, dix-neuf „zehn-neun“). Die Zahlen von 20 bis 69 werden ebenfalls transparent zusammengesetzt, wobei es eigene Wörter für die 20, 30, 40, 50 und 60 gibt, die den verwandten Einerwörtern lautlich ähneln aber nicht identisch sind (ähnlich wie im Deutschen und Englischen). Die Reihenfolge ist die der Dezimalschreibweise, wobei bei der 21, 31, 41, 51 und 61 ein et („und“) eingeschoben wird (z.B. vingt-et-un „zwanzig-und-eins“), bei anderen Einern aber nicht (z.B. vingt-deux „zwanzig-zwei“). Ein Wort für 70 gibt es nicht, hier zählt man einfach von der sechzig weiter aufwärts: 70 ist „sechzig-zehn“ (soixante-dix), 71 ist „sechzig-elf“ (soixante-et-onze, ein et wird eingeschoben), usw. Ein Wort für 80 gibt es auch nicht, hier sagt der Franzose „vier-zwanzig“ (quatre-vingt), bei der 81 wird hier ausnahmsweise kein et eingeschoben (quatre-vingt-un). Ein Wort für 90 fehlt dann ebenso, auch hier zählt man einfach weiter hoch: 90 ist „vier-zwanzig-zehn“ (quatre-vingt-dix), 91 ist „vier-zwanzig-elf“ (quatre-vingt-onze, anders als bei der 71 wird kein et eingeschoben. Ab 100 wiederholt sich dann der Irrsinn mit weiteren Überraschungen, die ich hier nicht ausbreiten möchte.
Wenn es ein Zahlensystem gibt, das mathematische Fähigkeiten ernsthaft behindern sollte, dann das französische. Das ändert nichts daran, dass Frankreich im PISA-Test 2000 und 2003 sowohl Deutschland als auch die USA klar geschlagen hat, und erst 2006 von Deutschland überholt wurde (die USA aber immer noch besiegte). Und dass die Niederländer, deren Zahlensystem exakt parallel zum Deutschen ist, die Japaner 2003 und 2006 schlugen, obwohl die japanischen Zahlwörter genau wie die chinesischen streng die Dezimalschreibweise imitieren.
Wer die Rechenkünste der Deutschen verbessern will, muss also den Mathematikunterricht verbessern. Die Sprache sollte er in Ruhe lassen.
MILLER, Kevin F., Catherine M. SMITH, Jianjun ZHU, Houcan ZHANG (1995) Preschool origins of cross-national differences in mathematical competence: The role of number-naming systems. Psychological Science 6.1: 56–60. [JSTOR]
HUMBOLDT, Wilhelm von (1836) Über die Verschiedenheit des menschlichen Sprachbaues und ihren Einfluss auf die geistige Entwickelung des Menschengeschlechts. Berlin: Königliche Akademie der Wissenschaften. [Google Books (Vollzugriff)]
SPIEGEL.de/DAMBECK, Holger (2010) Zwanzigeins schlägt einundzwanzig. Spiegel Online, 23. Februar 2010. [Link]
WHORF, Benjamin Lee (1956 [1941]). Languages and logic. In: John B. CARROLL (ed.), Language, thought, and reality. Selected writings of Benjamin Lee Whorf. London/New York: John Wiley and Sons [Urspr. erschienen in The Technology Review 43.6].
[Dieser Beitrag erschien ursprünglich im alten Sprachlog auf den SciLogs. Die hier erschienene Version enthält möglicherweise Korrekturen und Aktualisierungen. Auch die Kommentare wurden möglicherweise nicht vollständig übernommen.]

quatre-vingt
Angeblich soll es eine Kopfrechenaufgabe geben, die in französischen Grundschulen NIE gefragt wird:
4 x 20
Twenty-one
Bei Conan Doyles “Sherlock Holmes” findet sich ab und an die im Deutschen übliche Anordnung der Zahlwörter:
“now the spell had been upon him eight-and-forty hours”
“it is the first Saturday night for seven-and-twenty years”
“The man who entered was young, some two-and-twenty at the outside”
Dies ist aber nicht konsistent, auch die modernen Formen tauchen auf. Ein bestimmtes Muster hinter der Verwendung der beiden Formen habe ich nicht erkennen können. Weiss jemand mehr darüber? Danke!
one and twenty
@David Grellscheid: der OED schreibt dazu folgendes:
Combined with the numerals below ten (one to nine) to express the numbers between twenty and thirty; formerly (and still occasionally) one and twenty, two and twenty, etc. (rarely twenty and one, etc.); now commonly twenty-one, twenty-two, etc.; similarly with the ordinals from first to ninth, forming the ordinals corresponding to the above (twenty-first, twenty-second, etc.), in modern use substituted for the earlier one-and-twentieth, two-and-twentieth, etc. (see TWENTIETH A. 1c).
Die Date-Chart dazu gibt Werte von Ende 9. Jh bis Mitte 19. Jh. an.
Aber, wer wird denn hier wertend über Sprache urteilen?
Nebenbei, diese angeblichen Belege für eine schwache Relativitätshypothese kamen mir schon im Psychologiekurs mehr als suspekt vor. Ich bring es nicht mehr ganz zusammen, irgendwie ging es um die Frage nach einem Zusammenhang zwischen dem Genus eines Wortes und der Frage, ob man dieses Wort eher mit einem männlichen oder eher einem weiblichen Akteur in Verbindung bringen würde. Vielleicht ist A.S. (oder irgendwer anders) hier besser informiert und kann nochmal ein konkretes Beispiel anführen? Für mich stellt sich bei solchen Studien jedenfalls immer wieder die Frage nach dem Zusammenhang zwischen Kookkurrenz und Kausalität.
Auch, um beim eigentlichen Thema zu bleiben, war der Psychologiedozent der Auffassung, dass es Studien gibt, die tatsächlich belegen, dass das “deutsche” (i.e. relativ unregelmäßige) Zählsystem tatsächlich für erheblich mehr Verarbeitungsschwierigkeiten sorgen soll als ein vergleichsmäßig einfach gehaltenes Zählsystem wie im Chinesischen. Da hat man aber nicht auf den Output geguckt (wie in der hier diskutierten Studie) sondern direkt auf die Verarbeitung im Gehirn mit Hilfe von bildgebenden Verfahren selbst.
Vielleicht wäre es noch interessant zu erwähnen, warum wir im Deutschen einundzwanzig und nicht zwanzigeins oder zwanzigundeins sagen: Das hat primär prosodische Gründe: Das Betonungsmuster von Einundzwanzig ist ein perfekter Trochäus, wohingegen Zwanzigeins einen nicht-binären Fuss enthält, und Zwanzigundeins Trochäus und Jambus vermischt (bzw. eine ungeparste Silbe enthält), was in der deutschen Phonologie eher suboptimal ist. Ausnahmen davon betreffen Zahlwörter mit sieben, da das Wort sieben per se zweisilbig ist. Aber auch hier werden tendenziell eher Strategien angewendet, Silben zu unterdrücken, als die rythmische Struktur kaputt zu machen.
@Herzkoenig Was Sie als ‘Gewohnheit’ bezeichnen ist historische Kontingenz. Auch wenn Philosophen üblicherweise natürliche sprachen nutzen, sind die [Sprachen, nicht die Philosophen] keine logischen Konstrukte, sondern über Jahrhunderte, ja, Jahrtausende evolutionär gewachsene tonale Kommunikation. Übrigens genau der Grund, weshalb die philosophische Disziplin Logik immer wieder mal eigene Zeichensysteme entwickelt, und weshalb Mathematik uns schwieriger dünkt als, sagen wir, Aufsatzschreiben.
Was spricht dagegen, auf Krampf unser natursprachliches Zahlensystem zu ändern? Es würde mindestens 2, eher drei oder mehr Generationen benötigen. In diesem Land haben wir ja schon Schwierigkeiten eine sanfte Korrektur problematischer Rechtschreibung durchzuführen — oder die Ligatur ‘ß’ abzuschaffen.
Wales
Mal wieder ein sehr interessanter Artikel, danke dafür. Mich würde nur noch ein kurzer Kommentar zu dem folgenden Abschnitt aus dem spiegel.de-Artikel interessieren:
“Dass ein solcher Wechsel möglich ist, zeigt das Beispiel Wales. Dort wurde schon vor über 150 Jahren ein kompliziertes durch ein einfacheres System ersetzt. ”
Weiß dazu jemand etwas Genaueres?
xtrblk meint: Gelernt ist gelernt
Interessante Aufklärung. Das mit dem angeblichen Handicap durch “ein-und-zwanzig” statt “zwanzig-eins” etc. fand ich schon immer dubios. Wenn ein Kind die Zahl einmal gelernt hat, egal wie sie gebildet wird, und fleißig übt, kann es damit in jeder Variante problemlos rechnen.
Ähnliches wie für die Zahlen dürfte wohl auch für Wörter resp. Worbildungen gelten — s. die unregelmäßigen Verben in welcher Sprache auch immer. Man lernt das als Kind — und das ist es dann.
Ich würde sogar noch weiter gehen und vermuten, dass eine “schwierig konstruierte Sprache” wie das Deutsche ein besseres Intelligenztraining ist als eine “einfache Sprsache” wie Pidgin-English. Ob das so schwierige Deutsch uns Deutschen deshalb eine Weile den Ruf des Volkes der “Dichter und Denker” eingebracht hat?
Apropos “xytrblk”: Ich habe mir vorgenommen, nach und nach alle SciLogs-Kollegen zu besuchen und meinen Kommentar mit dieser Floskel einzuleiten. Wer wissen will, was es mit diesem Kunstwort auf sich hat, kann es googeln — oder gleich meine Website mit dem entsprechenden Eintrag besuchen:
http://www.minotauros-projekt.de/…rojekt/xytrblk
Beste Grüße — Jürgen vom Scheidt
Rechnen und Zahlenfolge
Wenn es einen sprachlichen Einfluß auf die Rechenfähigkeit gäbe, so sollte die Reihenfolge in den deutschen Zahlwörter das Kopfrechnen eigentlich erleichtern, da sie der Reihenfolge bei einfachen Rechenarten entspricht. Beim Addieren, Subtrahieren und Multiplizieren fängt man mit den Einern an und geht dann zu den Zehnern über (ggf. mit “x im Sinn”. Nur beim Dividieren fängt man mit den höheren Ziffern an. Mehrstellige Zahlen werden aber selten im Kopf dividiert.
Norsk, starke Verben und Humboldt-Zitate
Ich wollte an dieser Stelle eigentlich auch auf das Norwegische hinweisen, wo eine solche Veränderung vom “unlogischen” deutschen System zum “logischeren” englischen System ja tatsächlich stattgefunden hat. AS behauptet, daß dies in der Sprechergemeinschaft nicht wirklich angekommen ist. Gibt es dafür Belege? Ich habe auf die Schnelle nur einen Sprachkurs gefunden, der behauptet, daß das neue Zahlsystem heutzutage von den meisten Sprechern verwendet wird.
Vielleicht auch noch interessant für einige ist, daß es nicht nur Bewegungen zur Sprachvereinfachung gibt. Auch die umgekehrte Richtung hat ihre Verfechter, z.B. die Gesellschaft zur Stärkung der Verben.
Und wie Kristin fand ich es auch bemerkenswert, wieviele der Tagungs-Zitate ich hier in diesem Artikel wiederfand. Offenbar wirkt so eine mehrtägige Tagung auch mehrere Tage nach. 😉
Humboldt-Zitate
@kreetrapper, Kristin: Ja, ich habe mich über den Artikel auf Spiegel Online natürlich gefreut, weil er mir einen Anlass geboten hat, die schönen Whorf- und Humboldt-Zitate, mit denen auf der Konferenz etwas inflationär um sich geworfen wurde, gleich konkret anzuwenden. Kristin, dass Sie inkognito geblieben sind, ist aber nicht nett! Kreetrapper hat sich ordentlich vorgestellt…
@Kreetrapper: Ich habe irgendwo gelesen, dass die reformierten norwegischen Zahlenwörter zumindest für ältere Sprecher/innen immer noch eine technischere Konnotation hätten als die traditionellen, dass man also z.B. Altersangaben tendenziell noch eher nach dem alten System formulieren würde (das passt ja auch zu den Beobachtungen aus dem Englischen). Wenn ich beide Formen der norwegischen Zahlwörter auf .no-Webseiten suche, bekomme ich immer ungefähr ein Verhältnis von 1:10 (alt:neu), aber ich kann nicht genug Norwegisch, um zu beurteilen, um was für Treffer es sich handelt, wie das ganze mit Bokmål und Nynorsk zusammenhängt, oder ob überhaupt dänische Treffer dazwischen sind.
Taschenrechner
Mir fällt häufig auf, dass, wenn ich eine Zahl in einen Taschenrechner einzigeben versuche, während ich sie in meinem Kopf aufsage, ich sie falschherum eintippe. Ich denke “Ein-und-Zwanzig” und tippe eben in dieser Reihenfolge.
Tja, da aber die grafische Anordnung von Ziffern genau so arbiträr ist wie Zahlwörter ansich ist dies wohl einfach ein klarer Fall von Pech gehabt.
Wobei der Verein Zwanzigeins das sicher anders sieht 😉
@A.S.: Ich hab mich nicht getraut. Gelobe aber Besserung.
norsk tellemåte
@kreetrapper, A.S.: Mein Eindruck aus Norwegen ist, dass die unterschiedlichen Zählweisen nicht nur altersmäßig sondern vor allem auch geographisch stark varieren. So wird im Bergenser Dialekt fast ausschließlich “enogtyve” (21) gezählt (auch von jungen), während diese Zählweise in Oslo vielleicht auf die Generation 70+ beschränkt ist. Interessanterweise wird im Umland von Bergen in den traditionellen Nynorskregionen eigentlich nur “tjueein” oder “tjugeein” gezählt was vielleicht dafür spricht, dass die deutsche Zählweise eher ein Import aus dem Niederdeutschen via Hanse ist und kein alter Zug des Norwegischen. Ebenso dafür sprechen würde meiner Meinung nach, dass die Isländer “tuttugu og einn, tuttugu of tveir” etc. zählen (ich weiß allerdings nicht ob das im Altisländischen auch schon so war)
arabische Zahlen
Die gleiche Reihenfolge der Ziffern wie im deutschen findet man im Arabischen. Da unser Zahlensystem von den Arabern übernommen wurde (obwohl es diese widerum “indische Zahlen” nennen), nehme ich eher an, dass man darin die Ursache unserer Reihenfolge findet anstatt im Sprachrhythmus.
Übrigens ist die Deklination der Zahlen und gezählten Wörter im Arabischen noch komplizierter als im Russischen, so dass man annehmen könnte, dass die russische Grammatik auch vom Arabischen beeinflusst wurde.
Zitat: “Dank eines einfacheren Zahlensystems können sie schon früh besser zählen und rechnen.”
Vielleicht kann ich ein wenig Material zur Empirie aus Seitensicht hinzufügen: Am RoboCupJunior 2006 in Bremen haben die besten der besten 12- bis 19-jährigen Konstrukteure und Programmierer Fußball spielender autonomer Roboter teilgenommen, sie kamen aus China, den USA, Japan, Iran, Deutschland und mehr Ländern. Ich war als Schiedsrichter beteiligt. Die chinesischen Jugendlichen, obwohl in größter Zahl angereist, waren definitiv nicht besser als die anderen. Ihre Programme — in dem Alter geht es noch um Rechnen, nicht um Mathematik — waren einfacher gestrickt, die Resultate deshalb nicht besser als die der anderen.
nicht immer auf Frz. einschlagen
Wieso wird immer Französisch als Beispiel für ein kompiziertes Zahlwortsystem herangezogen? Wie wär’s mal mit Dänisch?
Die Wurzeln für 3 und 4 kommen in den “Zehner-Wörtern” mehrfach vor:
30 — treve
40 — fyrre
50 — halvtreds (halb dreimal [20])
60 — treds (dreimal [20])
70 — halvfjerds
80 — fjerds
90 — halvfems
100 — fems
Das, zusammen, mit der “deutschen” Stellung der Einer, macht es an der Supermarktkasse für den Ausländer, der die Sprache nur schlecht spricht, nicht einfacher. DEK 76,25 sind dann “sex og halvfjerds fem og tyve”. Was ist dagegen schon “soixante-six vingt-cinq”?
hoppla
Das musste ja passieren, und deshalb gleich hinterher: 76,25 sind auf Frz. natürlich “soixante-seize vingt-cinq”.
Die verflixte 7
Herr Stefanowitsch, Sie schreiben: “Wenn es ein Zahlensystem gibt, das mathematische Fähigkeiten ernsthaft behindern sollte, dann das französische. Das ändert nichts daran, dass Frankreich im PISA-Test 2000 und 2003 sowohl Deutschland als auch die USA klar geschlagen hat (…)”
Dafür kann es eigentlich nur eine Erklärung geben: Die französische 7 (sept) hat, wie im Chinesischen, nur eine Silbe:
Spiegel: “Mandarin-Zahlen haben gleich mehrere Vorteile: Erstens ist da die Kürze der Zahlwörter. Die chinesische 7 (qi) hat eine Silbe, beim englischen Seven und der deutschen Sieben sind es zwei.”
Die kurze 7 wiegt solche Extravaganzen wie ‘quatre-vingt’ sicher locker auf. 😉
Und diese Finnen machen die schöne Theorie mit ihrer dreisilbigen 7 (seitsemän) und Zahlwörtern, in denen jedes Glied durchdekliniert wird, kaputt.
versiebent
@GSchöfl
Sehr interessant. Danke für die Information. Ich finde, das schreit geradezu nach einer Korpusanalyse. Anatol, ich schlage vor, das auf die Liste mit Bachelorarbeitsthemen zu setzen.
@Kristin
Ich fand’s auch schade, daß man sich nicht kennengelernt hat. Vielleicht
können wir ja bei der nächsten (DGfS-)Tagung ein kleines Sprachblogger-Treffen organisieren.
@Almut
Die Idee mit der phonologischen Länge der Sieben gefällt mir. Die Finnen kann man sicher irgendwie wegerklären, Sprachen, die mehr Kasus benutzen als der Mensch Finger hat, sind doch sowieso höchst fragwürdig.
@kreetrapper: Aber gerne. Aus dem StuTS-Alter bist Du wahrscheinlich schon raus? (Demnächst findet die siebenundvierzigste statt, nur um hier beim Thema Zahlen zu bleiben.)
I don’t know how, I don’t know when…
@Kristin: Ja, auf der StuTS würden sie mich wohl nicht mehr reinlassen. Aber es wird sich sicher noch eine Gelegenheit ergeben. Vielleicht gehe ich auf die Summer School in Leipzig, die bei Dir im Blog auch als “Hinfahren” markiert ist, aber sicher ist das noch nicht.
Millionen
Bei größeren Zahlen erfordert das Übersetzen zwischen europäischen Sprachen und Chinesisch höhere Mathematik, denn im Chinesischen gibt es keine einfachen Wörter für Millionen und Milliarden. Solche Zahlen werden auf der Grundlage von wàn 万【萬】 „zehntausend“ ausgedrückt: 1 Million = bǎiwàn 百萬 „hundert(mal) zehntausend“ etc. – eine unerschöpfliche Quelle von Übersetzungsfehlern.
Entwicklung in Englisch
Ich bin auf den Artikel gestoßen und auf die dazugehörige Diskussion — die ich persönlich noch interessanter finde.
Aber zurück zu dem, weshalb ich eigentlich hier schreibe. Primär geht es um den Vorschlag die Entwicklung der Zahlsprechweise in der Englischen Sprache doch mal als BA Arbeit zu beleuchten.
Dies habe ich getan, nicht als BA Arbeit, aber als Arbeit im ersten Staatsexamen.
Der Grund für die Änderung liegt meines Erachtens nicht in dem Einfluss der franz. “Eroberer”, sondern vielmehr in der Verbreitung der arabischen Ziffern und somit der Eindeutigkeit bei der Dezimalschreibweise.
Linguistische Veränderungen brauchen immer Zeit und gerade bei Traditionalisten (Holmes ist entsprechend von Doyle angelegt) ist die Bereitschaft zur Veränderung geringer, bzw. es wird sich auf alte Traditionen zurück besonnen. Daher auch das auftreten der ungewohnten englischen Sprechweise.
Zweiter Grund für eine “ungewöhnliche” Sprechweise sind regionale Identitätsmerkmale bei Bevölkerungen (so gibt es die uns so vertraute Zahlform in einigen ländlichen Gegenden in England noch immer).
Das ganze zeigt aber auch noch etwas anders. Verwirrungen und Missverständnisse treten viel seltener auf, als man denkt. Also würde eine Änderung der Zahlworte das Land nicht ins Chaos stürzen.
Im Zusammenhang mit meiner Staatsarbeit kann ich mich auch noch an Artikel von Dehaene, Nuerk oder Willmes erinnern, die sich alle mit der “Verarbeitung” von Zahlen und Zahlworten im Gehirn beschäftigt haben (leider habe ich die Artikel momentan nicht zur Verfügung).
So erinnere ich mich noch an einen beschriebenen Effekt, dass im französischen ein Unterschied bei der Geschwindigkeit der Verarbeitung feststellbar ist, wenn das Zahlwort “verdreht” (also nicht identisch mit der Schreibweise der Zahlzeichen) benutzt wurde.
Abschließend noch eine Aussage zum letzten Teil des Artikels. Eine Änderung des Mathematikunterrichts hat es gegeben, zumindest bei motivierten Kollegen. Das der gewünschte Effekt (d.h. besseres abschneiden bei PISA und Co) sich noch nicht einstellt mag einige Gründe haben, vielleicht auch den Grund, dass das Schulsystem keine marode Bank ist…
@F. Althoff:
Danke für die Information. Ich interessiere mich sehr für dieses Thema und würde mich sehr freuen, wenn Sie mir Ihre Staatsarbeit oder wenigstens die Liste, der von Ihnen verwendeten Literatur, irgendwie zukommen lassen könnten. Kontaktieren Sie mich am besten per E‑Mail unter kreetrapper blutiges-gemetzel.de
Zurück zu den römischen Zahlen
Ich habe selbst oft genug erlebt, wie Schüler einfach ein richtiges Rechenergebnis falsch herum aufgeschrieben haben und deswegen Punkte in einem Test abgezogen bekommen haben, etwa
8*8=46
Das passiert den Schülern immer wieder, auch wenn sie ihr Problem kennen. Klar lernen sie es irgendwann, aber es bleibt auch für Erwachsene umständlich.
Es wäre eine relativ einfache Sache, die Sprechweise umzudrehen. Zwanzigeins und einundzwanzig können gerne nebeneinander bestehen. Wo ist also das Problem?
Das größte Hemmnis ist sicher die Gewohnheit. Da möchte ich aber nicht wissen, wie schwer es war, die römischen Zahlen durch die arabischen/indischen abzulösen oder auf das SI-Einheitensystem umzustellen. Aber vom heutigen Zustand aus betrachtet: Würde jemand zu römischen Zahlen oder zu Meilen und Ellen zurückwollen?
metric martyrs
@Dr.-Ing. Lämm
Ja, gibt’s genug von. Oder zumindest welche die das alte System auf jeden Fall beibehalten wollen. Einfach mal nach “metric martyrs” googlen.
Anekdote
Ich war mal in China im Zug unterwegs (Hartbettabteil, d.h. 6 Personen auf engstem Raum). Mir gegenüber eine junge Familie, die Tochter schätzungsweise 5–6 Jahre alt. Irgendwie sind wir drauf gekommen, dass sie Rechenspielchen mit mir machen wollte. Sie fragte mich, was denn 600 plus 600 sei. Ich antwortete: “Eintausend-zweihundert (Yi4 Qian1 er4 bai3)”. Sie schüttelte den Kopf und konnte es nicht fassen, dass ein erwachsener Mann nicht rechnen kann, und korrigierte mich in: “Zwölfhundert (Shi2 er4 bai3)”. Ich gab dann zu, dass ich ein “Strohsack (cao3bao3)” sei und deshalb nicht richtig rechnen könne.
Das Beispiel zeigt jedenfalls, dass es auch im Chineischen Zählvarianten gibt, die im Laufe der kindlichen Entwicklung nicht gleichzeitig gelernt werden.
Zweite Anmerkung: Die Zahl “zwei” bereitet im Chinesischen mitunter Probleme, da es für sie zwei verschiedene Worte gibt: “er4” und “liang3”. Die Regeln, wann welche Form verwendet wird, sind nicht ganz trivial. Manchmal ist eine der beiden Formen obligatorisch, manchmal wahlweise beide möglich. Die Zahl “200” wird i.d.R. durch “liang3 bai3” ausgedruckt. Die 200 in der Zahl “1200” lautet aber normalerweise “er4 bai3”.
Wales (Kymrisch)
Zunächst herzlichen Dank für den interessanten Blog generell und diesen Artikel im speziellen.
@Marcel S
Nachdem hier noch niemand zum Kymrischen (Walisisch) geantwortet hat, erlaube ich mir einmal, in die Tasten zu greifen.
In den keltischen Sprachen sind die Zahlwörter ja noch viel “schöner” als z. B. in den zitierten französischen Beispielen. Das Vigesimalsystem ist hier, zumindest in der traditionellen Zählweise, noch viel klarer erhalten (die französischen “Spezialitäten” könnten ein Rest des keltischen Substrates sein, das ist aber meines Wissens nach umstritten).
Im Kymrischen (Walisischen) sind die Zahlwörter von un (1) bis deg (10) ebenso Reflexe der indogermanischen Zahlwörter wie die deutschen. Diesbezüglich keine Besonderheiten.
Dann wird es sehr bunt (ich lasse die Flexion nach dem Genus und bestimmte Veränderungen ja nach Kontext der Einfachkeit halber beiseite):
un ar ddeg (11), wörtlich: “eins auf zehn”
deuddeg (12), wörtlich: “zwei (dau) zehn (deg)”
tri ar ddeg (13), wörtlich: “drei (tri) auf zehn”
pedwar ar ddeg (14), “vier (pedwar) auf zehn”
pymtheg (15), “fünf (pump) zehn”
Jetzt eine Überraschung:
un ar bymtheg (16), “eins auf fünfzehn”
dau ar bymtheg (17), “zwei auf fünfzehn”
und wieder etwas Extravagantes:
deunaw (18), wörtlich: “zwei (dau) neun (naw)”
pedwar ar bymtheg (19), “vier auf fünfzehn”
ugain (20)
Bis dreißig geht es jetzt ähnlich weiter wie im Deutschen,
z.B. dau ar hugain (22), “zwei auf zwanzig”
Dann aber konsequent weiter:
deg ar hugain (30), “zehn auf zwanzig”
un ar ddeg ar hugain (31), “eins auf zehn auf dreißig”
Ab deugain (40), “zwei zwanzig”, ist dann die Verbindung leicht anders,
z.B. naw a deugain (49), “neun und zwei zwanzig”, daher auch keine Lenition (Veränderung des Anlautes, hier deg -> ddeg) mehr (aber eventuell Aspiration; siehe unten, z.B. trigain -> thrigain).
Man kann im Prinzip ab fünfzig weitermachen zur Basis vierzig wie oben, gebräuchlicher ist aber hanner cant (50), “halb Hundert”, hanner cant ac un (51), etc.
Ab trigain (60) dann wieder wie zu erwarten, z.B. un a thrigain (61), pedwar ugain (80), pedwar ar bymtheg a phedwar ugain (99).
In sehr gehobenem, literarischen Stil konnte man übrigens auch Subtraktionszahlen verwenden, z.B.
deugain namyn un (39): “zwei zwanzig weniger eins”
deugain namyn tri (37)
Daneben gibt es ein neueres, dezimales Zählsystem, bis 10 natürlich gleich wie die alte Zählweise, darüber aber dann ganz “regelmäßig” vereinfacht, z.B.:
11 — un deg un
12 — un deg dau
54 — pum deg pedwar
199 — cant naw deg naw
Das dezimale System ist jüngeren Datums, tauchte im 19. Jh. auf, verbreitete sich aber wohl erst in der 2. Hälfte des 20. Jh. deutlich.
Peter Wynn Thomas, “Gramadeg y Gymraeg”, 1996, schreibt daß beide Systeme von der Mehrheit der Sprecher verwendet werden und daß die Wahl des System von einer Anzahl soziolinguistischer Faktoren abhänge und behandelt dies dann auf Seiten 299 und 300 (wenn jemand nachlesen möchte). Interessant ist, daß bei Angaben der Tageszeit ausschließlich das vigesimale System verwendet wird.
Auch David A. Thorne, A Comprehensive Welsh Grammar, 1993, S. 148, schreibt “The forms un deg un, wyth deg, wyth deg tri […] etc. are frequently used when giving the numbers of pages and hymns, to indicate the scores of games, in teaching mathematics, and increasingly in other contexts.”
Relativ ähnlich werden die Zahlen übrigens im Bretonischen nach dem Vigesimalsystem gebildet. Interessant die Abweichung bzgl. 18, das ist im Bretonischen nicht zweimal neun, sondern dreimal sechs, triwec’h.
Franz. Zahlen zum 2.
Die Schweizer/Belgischen Varianten der französischen Zahlwörter sind mir aus der Praxis bekannt; als sie mir in einer Orchesterprobe das erste Mal unterkamen, fragte ich in der Pause den Dirigenten (aus Fribourg), ob das eine Schweizer Eigenheit sei, was dieser bejahte. Er fügte auch hinzu, dass er, wenn er in Frankreich arbeitet sich bei den Französischen Varianten gelegentlich “verrechnet”, also Wörter wie cinquante-seize konstruiert und damit bei den Franzosen für einige Verwirrung sorgt.
Herr Stefanowitsch,
_soo_ einfach ist das mit den französischen Zahlen denn doch nicht. 🙂 Es gibt sehr wohl eigene Wörter für 70, 80 und 90, nämlich septante (Belgique, Suisse, est de la France, Acadie), huitante (Suisse; officiel dans le canton de Vaud), nonante (Belgique, Suisse). Diese Wörter werden ohne weiteres von Franzosen verstanden, aber üblicherweise nicht gebraucht. Lt. meinen schweizer Kollegen sind dies die während der französischen Revolution festgelegten offiziellen Zahlwörter. Ich kann dies nicht belegen, es erscheint mir aber wegen der innewohnenden Logik glaubhaft. Die Verbreitungsgebiete der Wörter habe ich aus dem Petit Robert auf CD von 1997.
PS: Ihre Artikel sind immer lesenswert. Danke dafür.
Ich weiß nicht, warum für Deutsche ausgerechnet immer das französische Zahlensystem als “pathologisches” Beispiel herhalten muss, wo es doch auch andere Kandidaten gibt. Im Russischen ziehen die Ziffer 1 den Nominativ Singular, die Ziffern 2 bis 4 den Genitiv Singular und alle anderen Ziffern den Genitiv Plural nach sich. Entsprechend werden dann die Bestandteile zur Bildung von Zehnern und Hundertern und das Substantiv für Tausend innerhalb(!) einer Zahl dekliniert. (200 hat nochmal eine eigene Form.) Zwischendurch begegnet einem außerdem ein völlig unregelmäßiges Wort für 40, das eine umstrittene Etymologie, aber überhaupt keine Beziehung zu 4 oder 10 hat.
Eine Blick auf die Zahlen 1 bis 100 in Hindi lässt befürchten, dass man sie alle auswendig lernen muss, oder sind die komplexen Assimilationen, die das zugrunde liegende regelmäßige Bildungsprinzip verzerrt haben, anderweitig ableitbar?
Was spricht eigentlich dagegen, dass man statt hundertfünfzehn hundertzehnfünf sagt? Eigentlich nur die Gewohnheit, oder?
In meinem früheren Beruf musste ich mehrmals am Tag lange Zahlenreihen ansagen (bzw. aufschreiben) und habe mich jedesmal darüber geärgert, weil diese unlogische Reihung den gesamten Arbeitsprozess verzögert hat.
@Herzkoenig
Beim Durchgeben der Wahlergebnisse eines Wahllokals sind wir vom Bezirkswahlamt Berlin — Pankow dazu angehalten, ziffernweise zu sprechen. Also statt »dreihundertneunzehn« sagt man einfach »drei eins neun«. Eine praktikable Lösung, ohne dass man die normale Sprache über den Haufen werfen muss. Im Übrigen bin ich der Auffassung, dass sich unsere Zahlenaussprache in den letzten Jahrhunderten verändert hätte, wenn sie tatsächlich so kompliziert wäre.
@Werner: Das ist ein interessanter Hinweis. Wer ernsthaft einen sprachlichen Einfluss auf mathematische Fähigkeiten untersuchen möchte, hätte mit den unterschiedlichen französischen Dialekten ein schönes Spielfeld.
@David Grellscheid, Simone: Ich habe zur Entwicklung der komplexen Zahlwörter im Englischen nicht viel gefunden, mir scheint sich hier wieder einmal ein schönes Thema für eine BA-Arbeit zu verstecken. Grundsätzlich entspricht die dem Deutschen parallele Sprechweise (seven-and-twenty years) dem ursprünglichen germanischen Muster. Dies war im Altenglischen die normale Art, komplexe Zahlwörter zu bilden. Durch den Einfluss des normannischen Französisch kam die heute übliche Sprechweise auf und verdrängte das ursprüngliche Muster, das sich bis ca. 1700 hielt [Weinstock 1999]. Es ist vermutet worden, dass der Wechsel zunächst bei den hohen Zahlen begann und sich nach unten vorarbeitete [Weinstock 1999] und eine informelle Korpusanalyse liefert eine erste Bestätigung [Diller 2005, S. 105]. Die ursprüngliche germanische Sprechweise hat sich bis heute in Dialekten gehalten, vor allem bei Alters- und Zeitangaben [Cahill und Gazdar 1997]. Das passt ja auch zu den Beispielen aus Sherlock Holmes.
CAHILL, Lynne und Gerald GAZDAR. 1997 A lexical analysis of numeral expressions in Dutch, English and German. [Link]
DILLER, Hans-Jürgen (2005) Rezension zu Weinstock 2003. Anglia — Zeitschrift für englische Philologie 123.2, S. 104–106.
WEINSTOCK, Horst (1999) Historical and comparative aspects of numerals between twenty-one and twenty-nine. In Uwe Carls und Peter Lucko (Hgg.), Form, function and variation in English: Studies in honour of Klaus Hansen. Frankfurt: Peter Lang, S. 65–77. [Neuabdruck 2003 in Horst Weinstock, Kleine Schriften: Ausgewählte Studien zur alt‑, mittel- und frühneuenglischen Sprache und Literatur. Heidelberg: Winter].
@Herzkoenig: Wenn man etwas ändern will, muss die Frage nicht lauten: „Was spricht eigentlich dagegen?“, sondern: „Was spricht eigentlich dafür?“. Und die Antwort in diesem Fall ist: „Nichts“. Die germanischen Sprachen haben mit der anti-dezimalen Sprechweise tausende von Jahren funktioniert und Sprachreformen sind selbst in reformgewöhnten Sprachgemeinschaften wie dem Norwegischen, wo die dezimale Sprechweise teilweise eingeführt wurde, fast immer aussichtslos. Für die konkreten Probleme beim Aufsagen von langen Zahlen gibt es die von Julius genannte Lösung, die sich ganz von allein entwickelt hat.
@Patrick: Die Studie zum Zusammenhang von Genus und Sexus bei Objekten stammt u.a. von Lera Boroditzky. Ich finde das, was ich dazu im Kopf habe, nicht mehr, aber die folgenden zwei Links passen auch dazu:
http://csjarchive.cogsci.rpi.edu/…3/pdfs/180.pdf
http://www-psych.stanford.edu/~lera/papers/
@A.S.: Das war schon eine humboldtzitatintensive Tagung, was?
Ich bin übrigens auch in Ihren Vortrag hineingegangen und danach klüger wieder daraus hinaus.
Linktipp: Einen thematisch ähnlichen Blogbeitrag zur Zählweise gab es auch von Günther M. Ziegler. Auch da auf Anregung vom Verein Zwanzigeins: Zehnersystem, Welterbe und Alternativen